コニファ・マメ知識:黄金比(Golden ratio)
黄金比(Golden ratio)とは
黄金比とは、自然界で最も美しく見えると言われている比率1: (1+√5)/2 です。
この比率で構成された長方形は黄金長方形と呼ばれます。縦1に対して、横が (1+√5)/2 になります。
この比率の近似値は、1:1.618となり、古くから西洋の絵画などに用いられています。黄金比が使われている身近なものとしては、名刺があります。

webデザインにおいても、この比率によるカラムレイアウトの分割(黄金分割)や、写真のトリミングのアスペクト比などに使われています。
黄金長方形の作図
紙の上で黄金長方形を描く場合、1:1.618の比率を使うほかにコンパスを使って作成することもできます。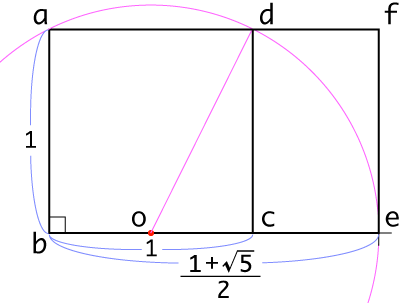
- 正方形を描き、1辺の線分bcの中心点oを求めます。
- 中心点oを軸にして、コンパスをaまたはdのサイズに延ばします。
- そのサイズで、oを軸にして円を描き、bcの延長線との交点eを求めます。
- 交点eから垂直に線を描き、線分adの延長線との交点をfとします 。
- abefの長方形が黄金長方形になります。